ඩක්වත්-ලුවිස් කියන්නෙ මොකක්ද? ඩක්වත්-ලුවිස් න්‍යාය හැදෙන්නෙ කොහොමද? ක්‍රිකට් තරග නරඹන බොහෝ දෙනෙක්ට කාලයක් පුරාවටම තියෙන ගැටලු තමයි මේවා.
තරගයක පිළිතුරු ඉනිම අතරවාරයේ දී කාලගුණයෙන් බාධාවක් ඇති වෙලා ආයෙත් පටන් ගන්න කිට්ටු වෙද්දි මුලින්ම අපි කල්පනා කරන්නේ හඹා යන කණ්ඩායමේ ඩක්වත් ලුවිස් ඉලක්කය කීයක් වෙයි ද කියන එක. කොච්චර ක්‍රිකට් පිස්සුවෙන් හිටියත් මේ ඩක්වත් ලුවිස් හැදෙන විදිහ ගැන බොහෝ දෙනෙකු දැනුවත් නැහැ.
ඉතිං අපි දීර්ඝ වශයෙන් බලමු මේ ඩක්වත්-ලුවිස් ක්‍රමවේදය ඇත්තටම හැදෙන්නෙ කොහොමද කියලා.
- ඩක්වර්ත්-ලුවිස් කියන්නේ මොකක්ද?
සීමිත පන්දුවාර ක්‍රිකට් තරගයක කාලගුණය හෝ වෙනත් කාරණාවක් මත නැවැත්වීමට සිදු වී තරග කාලය කෙටි වුවහොත් දෙවනුවට පන්දුවට පහර දෙන කණ්ඩායමේ ජයග්‍රාහී ලකුණු ඉලක්කය නිර්ණය කිරීම සඳහා වර්තමාන ක්‍රිකට් ලෝකයේ භාවිතා කරන ගණිතමය ක්‍රමවේදය තමයි ඩක්වර්ත්-ලුවිස් (DL method) කියලා හඳුන්වන්නේ.
2. ඩක්වර්ත් ලුවිස් මුලින්ම ක්‍රිකට් ක්‍රීඩාවට ආවෙ කොහොමද?
හා හා පුරාම කියලා ඩක්වත්-ලුවිස් (Duckworth–lewis method / DL) කියලා අලුතින් ක්‍රමවේදයක් 1997 වසරේ දී හඳුන්වලා දුන්නේ එංගලන්ත ජාතික සංඛ්‍යාලේඛණඥයන් දෙදෙනෙකු වන ෆ්‍රෑන්ක් ඩක්වර්ත් සහ ටෝනි ලුවිස් දෙදෙනා විසිනුයි. ඒත් 1999 වසරේ පටන් තමයි අන්තර්ජාතික ක්‍රිකට් කවුන්සිලයෙන් ඩක්වත්-ලුවිස් නිල ක්‍රමවේදය බවට පත්වුණේ.
මෙම ක්‍රමවේදය හඳුන්වා දීමට පාදක වුණු ප්‍රධානතම කාරණා තමයි ඒ වෙනුවට මීට පෙර භාවිතා කරපු ක්‍රමවේදයන් වුණු ලකුණු ලබා ගැනීමේ සාමාන්‍ය වේගයේ ක්‍රමවේදය (Average run rate method) සහ වඩා ඵලදායී පන්දුවාර ක්‍රමවේදය (Most productive overs method) යන ක්‍රම දෙකම එක් කණ්ඩායමකට පමණක් අතිශයින් අසාධාරණ වීම නිසා දැඩි ලෙසින් අසාර්ථකත්වයට පත්වීම යන හේතූන්.
ඒ ක්‍රමවේදයන් දෙකේ දී ම දැවී ගියපු කඩුලු ගණන නිර්ණායකයක් ලෙස පදනම් නොකරගැනීම තමයි ඩක්වර්ත්-ලුවිස් වගේ ආදේශකයක් ක්‍රිකට් ලෝකයට එන්න බලපාපු මූලිකම හේතුසාධකය බවට පත්වුණේ.
1997-2014 දක්වා කාල සීමාවේ දී මෙය ඩක්වර්ත්-ලුවිස් ක්‍රමය (DL method) ලෙස හැඳින්වූවත් ඉන්පසුව මෙය ඩක්වර්ත් ලුවිස් ස්ටර්න් (Duckworth–lewis–stern method / DLS) ලෙසින් මෙහි නම වෙනස් කිරීමකට ලක්වුණා.
මෙම ක්‍රමවේදයේ වර්තමාන භාරකරුවා වන මහාචාර්ය ස්ටීව් ස්ටර්න් Steven Sternට උපහාරයක් වශයෙන් තමයි ඒ විදිහට නම වෙනස් කිරීමකට ලක් වෙලා තිබෙන්නේ. එම වසර දක්වා භාවිතා වූ ඩක්වර්ත් ලුවිස් ක්‍රමවේදයට වඩා වර්තමානයේ භාවිතා වන මෙම ඩක්වර්ත් ලුවිස් ස්ටර්න් ක්‍රමවේදය ඔස්සේ පළමුව පන්දුවට පහරදුන් කණ්ඩායමට යම් වාසියක් හිමිව තිබෙනවා.
පරිගණක මෘදුකාංගයක් මගින් පමණක් එම සංශෝධනය සිදු කළ හැකි නිසා ස්ටර්න් ක්‍රමය පැහැදිලි කිරීමේ හැකියාවක් අපට නැහැ. කෙසේ වෙතත් ඉන් ලැබෙන පිළිතුර සහ මීට පෙර භාවිතා කළ ඩක්වර්ත් ලුවිස් සංශෝධනයේ පිළිතුර අතර ඇත්තේ ඉතාමත් සුළු වෙනසක් වන අතර මෙම සංශෝධනයන් දෙක පිටුපසම ඇත්තේ එකම න්‍යායකි.
ආසන්න වශයෙන් ලකුණු 1-3 අතර වැනි සුළු ගණනක වෙනසක් පමණක් මෙම සංශෝධනයේ දී සිදු වන අතර තරග ස්වභාවයට අනුව එය තීරණය වෙනවා.
අපි එම වෙනස්කම් ගැන පසුව උදාහරණ ද සමඟින් කතාකරමු.
3.ගණනය කිරීමේ සිද්ධාන්ත
ඩක්වත් ලුවිස් ගණනය කරන්න ප්‍රධාන වශයෙන්ම මූලික කරගන්නේ සම්පත් (resources).
මෙම සම්පත් කොටස් දෙකකින් සමන්විත වෙනවා. පන්දුවට පහර දෙන කණ්ඩායම සතුව ඉතිරි වෙලා තිබෙන,
3.1 පන්දුවාර සංඛ්‍යාව සහ
3.2 කඩුලු සංඛ්‍යාව
උදාහරණයක් විදිහට එක්දින තරගයක නම් පන්දු වාර 50 ක් හා කඩුලු 10 ක් තියෙනවා නම් අපි 100%ක් සම්පත් තිබෙන විදිහටයි සලකන්නේ.
හැබැයි ඩක්වර්ත් ලුවිස් ස්ටර්න් මගින් ඉහත කරුණු දෙකට අමතරව ඉනිමක් තුළ බාධා ඇතිවූ විට “තරගයට නැවත සූදානම් වීම සඳහා ගත වන කාලය” සඳහා මීට පෙර පැවති සංශෝධනයට වඩා වැඩි වටිනාකමක් ලබා දීලා තිබෙනවා.
ඒ කියන්නේ සාමාන්‍යයෙන් ඉනිමක් අවසානයේ පන්දුවාර කිහිපයක් අහිමි වීම මගින් ඉනිමක් ආරම්භයේ පන්දුවාර කිහිපයක් අහිමි වීමට වඩා පාඩුවක් සිදු වෙනවා. මොකද කියනවා නම් ඕනෑම කණ්ඩායමක් තම ඉනිම සැලසුම් කරන්නේ අවසන් පන්දුවාර කිහිපයේ වඩා ආක්‍රමණික ලෙස ක්‍රීඩා කරමින් වැඩි ලකුණු ප්‍රමාණයක් කණ්ඩායමට එක් කිරීමටයි.
නමුත් තරගය අතරමැද නැවැත්වීමට සිදු වෙලා යළිත් පිතිකරණයේ යෙදෙන අවස්ථාවේ පන්දුවාර සංඛ්‍යාව කෙටි වුවහොත් අපි ඒක “නැවත සූදානම් වීම සඳහා ගත වන කාලය (readjusting time)” ලෙසින් හඳුන්වනවා.
උදාහරණයක් විදිහට Team A සහ B අතර තරගයක දී Team A ඉනිමේ පන්දුවාර 25කට 150-2 ලෙස ලකුණු පුවරුවක් තිබෙද්දී වර්ෂාව පතිත වෙලා යළිත් තරගය ආරම්භ වෙද්දී තරගයේ පන්දුවාර 10ක් අඩු වුවහොත්, ඒ කියන්නෙ Team A ඉනිම පන්දුවාර 40කට සීමා වුනොත් එම කණ්ඩායමට වෙන්න පුළුවන් අසාධාරණය මගහරවා ගැනීමට මේ මගින් හැකියාවක් ලැබෙනවා. මොකද තරගය පන්දුවාර 40යි කියලා Team A මුල සිටම දැනගෙන සිටියා නම් ඔවුන් මීට වඩා වැඩි ලකුණු වේගයකින් මුල සිටම පන්දුවට පහර දෙනවා.
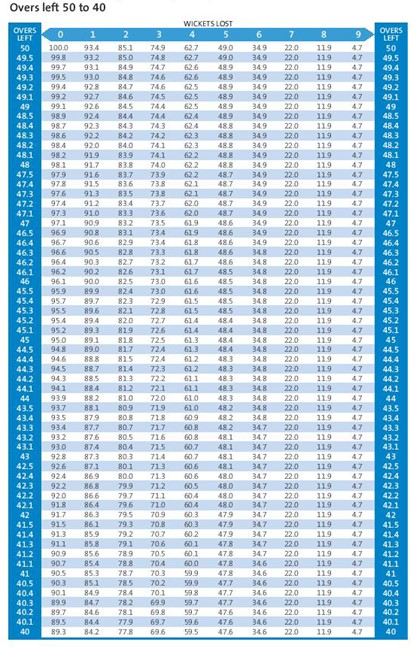
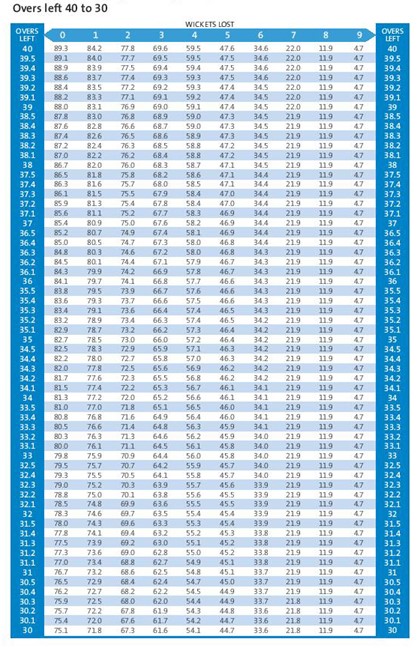
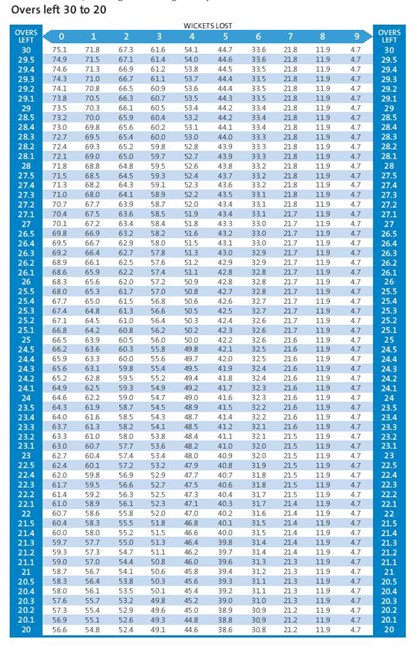
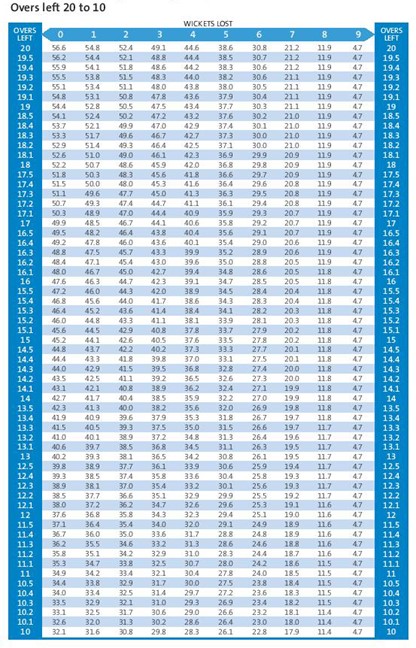
අපි දැන් බලමු අත ඉතිරි පන්දුවාර ගණනට අනුව අත ඉතිරි කඩුලු ගණනේ සම්පත් ප්‍රමාණය ප්‍රස්ථාරයක් මගින් දැක්වෙන්නේ කොහොමද කියලා.
ඉනිම ක්‍රීඩා කරගෙන යද්දී අතරමඟ නතර කිරීමට සිදු වුවහොත් දැමීමට ඉතිරි පන්දුවාර ගණන සහ අත ඉතිරි කඩුලු ගණන යනා දී සම්පත්වල ප්‍රතිශත මත තමයි දෙනු ලබන ජයග්‍රාහී ඉලක්කය ලබා දීම හෝ ජයග්‍රාහකයා තීරණය කිරීමට සිදුවන්නේ.
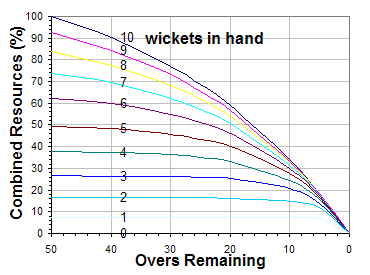
එම ප්‍රතිශතයන් හැදෙන්නෙ මෙන්න මේ වගුවට අනුවයි.
අපි මේක කොටස් වශයෙන් බලමු.
මේ මගින් මුල්පෙළ කඩුලුවලට වැඩි සම්පත් ප්‍රතිශතයක් ලැබෙනවා. ඒ කියන්නෙ මුල්පෙළ කඩුලුවලට වැඩි වටිනාකමක් එන විදිහට තමයි මෙම වගුවේ ප්‍රතිශතයන් දක්වලා තිබෙන්නේ.
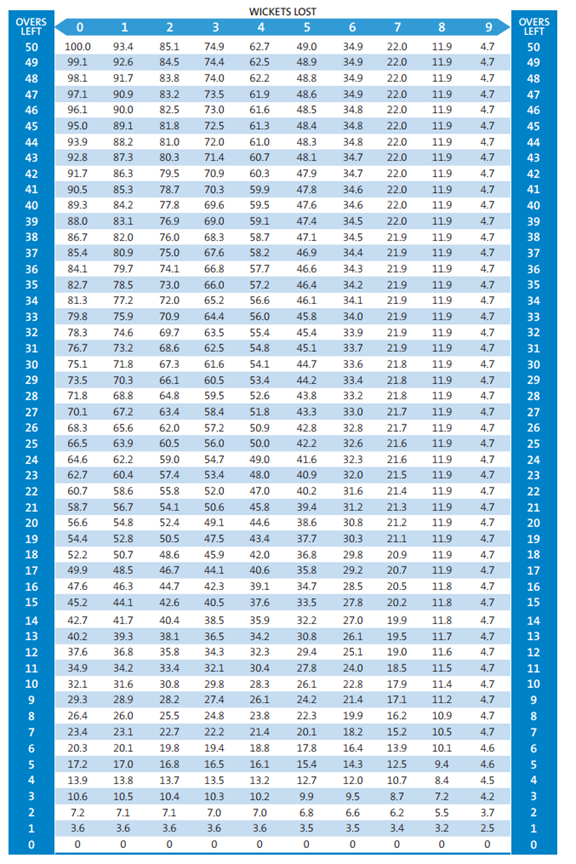
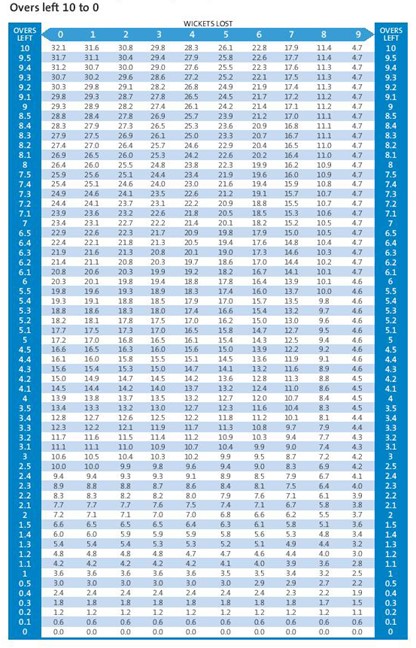
4.ඩක්වර්ත් ලුවිස් ක්‍රියාත්මක කරන්න පුළුවන් වෙන්නේ කොයි වගේ අවස්ථාවක දී ද?
දැන් අපි බලමු මෙම DL ක්‍රමවේදය ක්‍රියාත්මක කිරීමට හැකි වන්නේ කුමන අවස්ථාවක දී ද කියන එක. මෙහි දී දෙවනුවට පන්දුවට පහර දෙන කණ්ඩායම අවම වශයෙන් සම්පූර්ණ කළ යුතු නිශ්චිත පන්දුවාර ප්‍රමාණයක් තිබෙනවා.
පන්දුවාර 50 එක්දින තරගයක දී නම් පන්දුවාර 20ක් සහ පන්දුවාර 20 තරගයක දී නම් පන්දුවාර 5ක් අනිවාර්යයෙන්ම පන්දුවට පහර දී සිටියොත් පමණයි ඩක්වර්ත් ලුවීස් ක්‍රමවේදය ඔස්සේ අවසන් තීරණයක් ලබා දෙන්නේ කියලා අපි හොඳින් මතක තියාගන්න ඕන. එසේ වුණේ නැත්නම් තරගය කිසිදු තීරණයකින් තොරව අතහැර දැමීමට සිදු වෙනවා.
5.මොකක්ද මේ Par Score කියන්නේ?
තරගයක් අතරතුර දී සිදුවන බාධාවක් නිසා තවකාලිකව නවත්වලා නැවත වතාවක් ආරම්භ වෙද්දී පන්දුවාර සංඛ්‍යාව කෙටි වීමකට ලක්වුවහොත් ඒ අනුව එම කණ්ඩායමේ ජයග්‍රාහී ඉලක්කයත් වෙනස් වීමකට ලක්වෙනවා.
ඉන්පසුව ලබා ගත යුතු වෙන සංශෝධිත ජයග්‍රාහී ඉලක්කයට තමයි අපි “Par Score” කියලා කියන්නේ. ගොඩක් දෙනා ජයග්‍රාහී ඉලක්කය (Target) සහ Par score දෙක පටලවගන්න නිසා තමා මේ ගැන මුලින්ම කියන්න හිතුවේ.
මෙම Par score අගය ලබා ගන්නේ පූර්ණ සංඛ්‍යාවක් ලෙසින්. ඒ කියන්නේ අපි මේ සඳහා භාවිතා කරන සූත්‍රයෙන් සුළු කළාට පස්සෙ ලැබෙන පිළිතුරේ දශම සංඛ්‍යාවන් ඉවත් කරලා තමයි අපි අවසාන පිළිතුර ලබා ගන්නේ. අපි දැන් බලමු ඒ සඳහා යොදාගන්න සූත්‍රය මොකක්ද කියලා.
Par Score (සංශෝධිත ජයග්‍රාහී ඉලක්කය) = පළමුවට පන්දුවට පහර දුන් කණ්ඩායම ලබා ගත් ලකුණු * දෙවනුවට පන්දුවට පහර දෙන කණ්ඩායමේ සම්පත් ප්‍රතිශතය / පළමුවට පන්දුවට පහර දෙන කණ්ඩායමේ සම්පත් ප්‍රතිශතය
අපි දැන් උදාහරණයක් සමඟින්ම මේ ගැන කතා කරමු. ඒ අනුව අපි Team A හා Team B කියලා කණ්ඩායම් දෙකක් අතර තරගයක උපකල්පනයකට එමු.
මෙම තරගයේ මුලින්ම පන්දුවට පහර දුන්න කණ්ඩායම නියමිත පන්දුවාර 50 අවසානයේ දී කඩුලු පහක් ලකුණු 300ක් ලබා ගත්තා කියලා අපි හිතමු. ඉන් අනතුරුව තරගයට වර්ෂාවෙන් බාධා වෙලා Team B පන්දුවාර 25කට සීමා කරන්න වෙනවා කියලා අපි හිතමු.
මෙහි දී අපි Team A සම්පත් ප්‍රතිශතය විදිහට සලකන්නේ 100%ක්. ඊට හේතුව කොයිවිදිහකින් ඔවුන්ගේ හරි ඉනිම අවසන් වීම. Team B සම්පත් ප්‍රතිශතය හැදෙන්නේ ඔවුන් අත ඉතිරි කඩුලු සංඛ්‍යාව සහ පන්දුවාර සංඛ්‍යාවට අනුසාරයෙනුයි. ඒ කියන්නේ දැන් Team B සතුව කඩුලු 10ම සහ තවත් පන්දුවාර 25ක් ඉතිරි වෙලා තිබෙනවා. ඒ අනුව ඉහත වගුවෙන් අපට ලැබෙන සම්පත් ප්‍රතිශතය වෙන්නේ මෙතන 66.5%ක්.
අපි දැන් මේ සියලුම අගයන් ඉහත සූත්‍රයට ආදේශ කරලා බලමු.
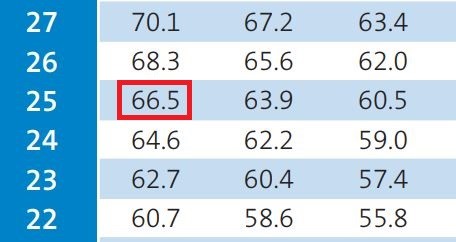
300 * 66.5% / 100% = 199.5
මෙහි දී ලැබෙන පිළිතුර ඊළඟ පූර්ණ සංඛ්‍යාවට වටයලා තමයි අපි සංශෝධිත ජයග්‍රාහී ඉලක්කය තීරණය කරන්නේ. ඒ කියන්නේ ලකුණු 200ක්. ලකුණු 199ක් ලබා ගත්තොත් තරගයේ ලකුණු සමවෙනවා. ඒ අනුව Team B වෙත පන්දුවාර 25ක දී ලැබෙන සංශෝධිත ජයග්‍රාහී ඉලක්කය (Par score) බවට පත්වෙන්නේ ලකුණු 200ක්.
- අඩසියවසක එක්දින තරග ආකෘතියේ යුග තුනක වෙනස
- සෙවාග් නම් වූ “ටෙස්ට්” පිතිකරුවා
- 2015න් පසු ක්‍රිකට් කොයිබටද?
- නායකත්වය වෙනම මානයකට රැගෙන ගිය අති විශිෂ්ටයා, “මහී”
- Photo Story – 15 වසරක් පුරාවට මාලිංග දැක්වූ වීරක්‍රියා
6. බාධා ඇති වූ තරගයක දෙවැනි ඉනිමේ ජයග්‍රාහී ඉලක්කය (Target) ගණනය කිරීම
බාධා වූ තරගයක ජයග්‍රාහී ඉලක්කය ගණනය කිරීමට සිදු වන අවස්ථා කිහිපයක්ම තිබෙනවා.
අපි පළමුව පන්දුවට පහර දෙන කණ්ඩායම Team A ලෙසත් දෙවනුව පන්දුවට පහර දෙන කණ්ඩායම Team B ලෙසත් උපකල්පනය කරමු.
- Team A ඉනිම අතරතුර තාවකාලිකව බාධා ඇතිවීම.
- Team B ඉනිම අතරතුර තාවකාලිකව බාධා ඇතිවීම.
- Team B ඉනිම අතරතුර බාධා වී යළි තරගය ආරම්භ කිරීමට නොහැකි වීම.
- Team B ඉනිම ප්‍රමාද වී ආරම්භ වීම.
- තරගයේ බාධා වීම් කිහිපයක් සිදුවීම.
- Team A ඉනිම අතරතුරදී බාධා ඇතිවී ඉනිම අවසන් කිරීමට සිදුවීම සහ Team B ඉනිම ආරම්භ වීමට ප්‍රමාද වීම.
මෙම අවස්ථාවන් 6 සඳහාම ඩක්වර්ත් ලුවිස් ගණනය කිරීම සඳහා යොදාගන්නා පොදු සූත්‍රයක් තිබෙනවා. ඒ තමයි,
T = (S x R2/R1) + 1 යන සූත්‍රය
T (Target) – ඉලක්කය
S (Score)- ලකුණු සංඛ්‍යාව (පළමුවට පන්දුවට පහර දුන් කණ්ඩායමේ)
R2 (Resource available for team batting second) – දෙවනුවට පන්දුවට පහර දුන් කණ්ඩායමට ඉතිරි වී ඇති සම්පත් ප්‍රමාණය
R1 (Resource available for team batting first) – මුලින් පන්දුවට පහර දුන් කණ්ඩායමට ඉතිරි වී ඇති සම්පත් ප්‍රමාණය
අපි මෙම අවස්ථා 6 උදාහරණ සමඟින්ම කථා කරමු.
6.1. Team A ඉනිම අතරතුර බාධා ඇති වීම.
2019 ලෝක කුසලානයේ මූලික වටයේ ශ්‍රී ලංකාව ඇෆ්ගනිස්තානය සමඟින් ක්‍රීඩා කරපු තරගය මේකට උදාහරණය විදිහට අපි අරගමු.
මෙම තරගයේ මුලින් පන්දුවට පහර දුන් ශ්‍රී ලංකා ඉනිමේ පන්දුවාර 33ක් අවසන් වන විට තරගයට වර්ෂාව පතිත වුනා. ඒ වන විට ශ්‍රී ලංකා ලකුණු පුවරුව සටහන් වූයේ 182/8ක් ලෙසයි. වර්ෂාවෙන් අනතුරුව තරගය පන්දුවාර 41කට අඩු වූ අතර එහි දී ශ්‍රී ලංකාව පන්දුවාර 36.5ක් තුළ දී සියලු දෙනා දැවී ලකුණු 201ක් රැස් කළා.
මෙහි දී වර්ෂාවෙන් බාධාවක් නොවුනා නම් ශ්‍රී ලංකාවේ ඉතිරි කඩුලු 2ත් ඉතා ඉක්මනින්ම දැවී යන්න වූනත් යම් අවකාශයක් තිබුණා. එම හේතුවෙන් තරගයේ පන්දුවාර සංඛ්‍යාව අඩු වුනාට පස්සේ ශ්‍රී ලංකාවට කඩුල්ලෙ රැඳිලා ඉන්න අවශ්‍ය වෙන්නේ තවත් පන්දුවාර 8ක් පමණක් වුණ නිසා වර්ෂාව හේතුවෙන් ශ්‍රී ලංකාවට අමතර වාසියක් හිමිවීමටත් ඉඩක් තිබුණා.
එහෙත් ඩක්වර්ත් ලුවිස් ගණනය කිරීම්හිදී දැවී ගිය කඩුලු සංඛ්‍යාවට අනුව ලැබෙන සම්පත් ප්‍රතිශතය වෙනස් වන නිසා ශ්‍රී ලංකාවට මෙහි දී වාසියක් හිමි වුනේ නැහැ.
එම නිසා ඩක්වර්ත් ලුවිස් සංශෝධනයට අනුව ඇෆ්ගනිස්තානය ලබා ගත යුතු ජයග්‍රාහී ඉලක්කය බවට පත්වුණේ පන්දුවාර 41ක් තුළ ලකුණු 187ක ඉලක්කයකුයි. අපි දැන් බලමු මේ 187 හැදුණේ කොහොමද කියලා.
ඩක්වර්ත් ලුවිස් සූත්‍රයට අනුව අපි මේ ඇෆ්ගනිස්තානුවන්ගේ ජයග්‍රාහී ඉලක්කය ගණනය කරන්නේ මෙන්න මෙහෙමයි.
Target = S * (R2 / R1) + 1
මෙම තරගයේ මුලින් පන්දුවට පහර දුන් ශ්‍රී ලංකාව ලබා ගත්ත ලකුණු සංඛ්‍යාව 201ක් නිසා අපි S වශයෙන් 201 නැමැති අගය සලකනවා.
දැන් අපි බලමු R1 හැදෙන්නේ කොහොමද කියලා,
පන්දුවාර 33ක දී වර්ෂාවෙන් බාධා ඇති වෙලා තරගය නවත්වන මොහොතේ ශ්‍රී ලංකා කණ්ඩායමේ ලකුණු පුවරුව සටහන් වුනේ කඩුලු 8ක් දැවී ලකුණු 182ක් ලෙසයි. ඒ කියන්නෙ ශ්‍රී ලංකාව සතුව එම මොහොතේ පන්දු වාර 17ක් සහ කඩුලු 2ක් අතැතිව තිබුණා.
ඒ අනුව මෙම වගුවෙන් ලැබෙන සම්පත් ප්‍රතිශතය වෙන්නේ 11.9%ක්.
ඒත් වර්ෂාවෙන් අනතුරුව තරගය පන්දුවාර 41කට සීමා වුනාට පස්සෙ ශ්‍රී ලංකාව අතැතිව තිබෙන්නේ පන්දුවාර 8ක් සහ කඩුලු 2ක් පමණයි. ඒ අනුව මෙම වගුවෙන් ලැබෙන සම්පත් ප්‍රතිශතය වෙන්නේ 10.9%ක්. ඒ අනුව මෙහි දී ශ්‍රී ලංකාවට අහිමි වන සම්පත් ප්‍රතිශතය වෙන්නේ 1%ක්.
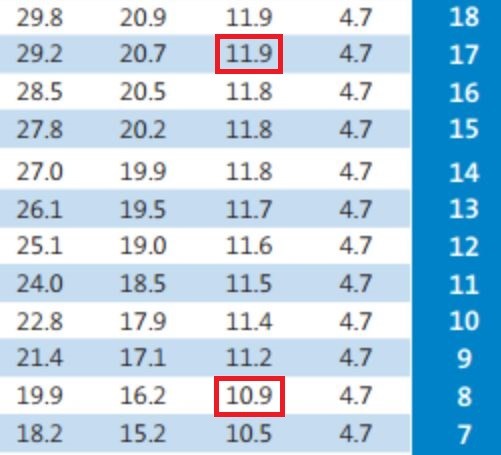
11.9 – 10.9 = 1
මෙහි දී ශ්‍රී ලංකාවට හිමි වන සම්පත් ප්‍රතිශතය ගණනය කිරීමට නම් අපි මේ අහිමි වුණු 1%ක සම්පත් ප්‍රතිශතය 100%න් අඩුකරන්න වෙනවා.
මේ අනුව ශ්‍රී ලංකාවට හිම්වන සම්පත් ප්‍රතිශතය බවට පත්වෙන්නේ 99%ක්.
දැන් අපි බලමු R2 හැදෙන්නේ කොහොමද කියලා,
මෙහි දී ඇෆ්ගනිස්තානය අතැතිව තිබෙන පන්දුවාර 41ක් සහ කඩුලු 10ක් අතැතිව තිබෙන නිසා මෙම වගුවට අනුව ඔවුන්ගේ සම්පත් ප්‍රමාණය වන්නේ 90.5%ක්
දැන් අපි ඒ අගයන් සියල්ලම මෙම සූත්‍රයට අන්තර්ගත කරමු.
201 * (90.5 / 99) + 1
මේ අනුව අපිට ලැබෙන පිළිතුර වන්නේ 184.71ක්.
මෙහි දී දශම ස්ථානයෙන් පසුව තිබෙන කිසිම අංකයක් ගණනය කිරීමකට ලක්වන්නේ නැති නිසා ඇෆ්ගනිස්තානයට ලැබෙන ඩක්වර්ත් ලැබුණු ජයග්‍රාහී ඉලක්කය වන්නේ ලකුණු 184ක්. නමුත් එදා ඔවුන්ට ලැබුණේ ලකුණු 187ක ඉලක්කයක්. ඒ තමයි මම කලින් සඳහන් කරපු පරිදි ඩක්වර්ත් ලුවීස් ස්ටර්න් සංශෝධනයට අනුව ලැබෙන පිළිතුර. ඒ අනුව ලකුණු 3ක වෙනසක් තමයි පරිගණක මෘදුකාංගය මගින් මීට එක්වෙලා තියෙන්නෙ.
6.2. Team B ඉනිම අතරතුර බාධා ඇති වීම.
අපි හැමෝගෙම මතකයේ වැඩියෙන්ම රැඳිලා තිබෙන තරගයක් තමයි 2007 ලෝක කුසලාන අවසාන මහා තරගය. වර්ෂාව සහ අයහපත් ආලෝක තත්ත්වය නිසා මෙම තරගයේ අවසන් භාගය ක්‍රීඩා කරන්න සිදු වුනේ අඳුරු කාලගුණ තත්ත්වයක් යටතේයි.
වර්ෂාව නිසා මෙම තරගයේ පන්දුවාර සංඛ්‍යාව 38ට සීමා වුණු අතර එහි දී ඕස්ට්‍රේලියාව ලකුණු 281ක් තම ලකුණු පුවරුවට එක්කළා. මෙහි දී ශ්‍රී ලංකා කණ්ඩායමට පන්දුවාර 38ක දී ලකුණු 282ක ජයග්‍රාහී ඉලක්කයක් හිමි වුනා.
එහෙත් පිළිතුරු ඉනිම ක්‍රීඩා කළ ශ්‍රී ලංකා කණ්ඩායමේ 25 වැනි පන්දුවාරයේ දී නැවතත් කාලගුණය හරස් වුනා. එහි දී ශ්‍රී ලංකා ලකුණු පුවරුව පන්දුවාර 24.5ක දී සටහන් වූයේ කඩුලු 3ක් දැවී ලකුණු 152ක් ලෙසයි.
එහෙත් වර්ෂාවෙන් පසු නැවතත් තරගය ආරම්භ වූයේ තවත් පන්දුවාර 2ක් අඩු කරමින්. ඒ අනුව ශ්‍රී ලංකාවට එදා පන්දුවාර 36ක් තුල ලැබුණු ඩක්වර්ත් ලුවිස් ඉලක්කය බවට පත්වුණේ ලකුණු 269ක්. අපි දැන් බලමු මේ 269 හැදුණේ කොහොමද කියලා.
කෙසේ වෙතත් යළි තරගය ආරම්භ කරනු ලැබුවේ පන්දුවාර 2ක් අඩුකරමිනුයි. ඒ කියන්නේ පන්දුවාර 36ක් තුළ ශ්‍රී ලංකාවට ලබා ගත යුතු ජයග්‍රාහී ඉලක්කය ලකුණු 269ක් බවට ඩක්වත්-ලුවීස් සූත්‍රයට අනුව සංශෝධනය වුනා.
ඩක්වර්ත් ලුවිස් සූත්‍රයට අනුව එය ගණනය කරන්නේ මෙන්න මෙහෙමයි.
Target = S * (R2 / R1) + 1
මෙම තරගයේ මුලින් පන්දුවට පහර දුන් ඕස්ට්‍රේලියාව ලබා ගත්ත ලකුණු සංඛ්‍යාව 281ක් නිසා අපි S වශයෙන් 281 නැමැති අගය සලකනු ලබනවා.
මෙහි දී ඕස්ට්‍රේලියානුවන්ගේ ඉනිම කිසිම බාධාවකින් තොරව නිමා කළ නිසා අපි ඔවුන්ගේ සම්පත් ප්‍රමාණය 100%ක් වශයෙන් සලකනවා. ඒ කියන්නෙ මෙතන R1 වෙන්නෙ 100%ක්.
දැන් අපි බලමු R2 හැදෙන්නේ කොහොමද කියලා,
පන්දුවාර 24.5ක දී වර්ෂාවෙන් බාධා ඇති වෙලා තරගය නවත්වන මොහොතේ ශ්‍රී ලංකා කණ්ඩායමේ ලකුණු පුවරුව සටහන් වුණේ කඩුලු 3ක් දැවී ලකුණු 152ක් ලෙසයි. ඒ කියන්නෙ ශ්‍රී ලංකාව සතුව එම මොහොතේ පන්දුවාර 13.1ක් සහ කඩුලු 7ක් අතැතිව තිබුණා.
ඒ අනුව මෙම වගුවෙන් ලැබෙන සම්පත් ප්‍රතිශතය වෙන්නේ 36.8ක්.
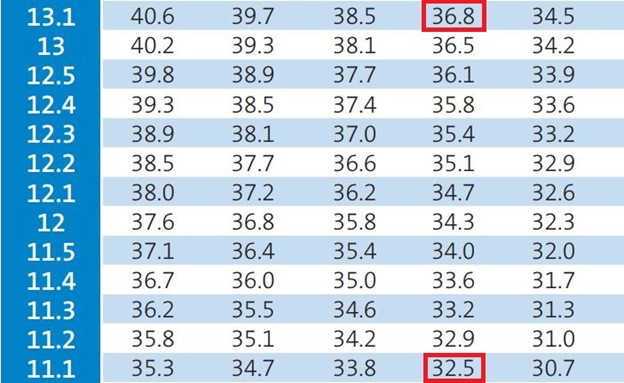
ඒත් වර්ෂාවෙන් අනතුරුව තරගය පන්දුවාර 36කට සීමා වුනාට පස්සෙ ශ්‍රී ලංකාව අතැතිව තිබෙන්නේ පන්දුවාර 11ක් සහ කඩුලු 7ක් පමණයි. ඒ අනුව මෙම වගුවෙන් ලැබෙන සම්පත් ප්‍රතිශතය වෙන්නේ 32.5%ක්. ඒ අනුව මෙහි දී ශ්‍රී ලංකාවට අහිමි වන සම්පත් ප්‍රතිශතය වෙන්නේ 4.3%ක්.
36.8 – 32.5 = 4.3
ශ්‍රී ලංකාවට හිමිවන සම්පත් ප්‍රතිශතය ගණනය කිරීමට නම් අපි මේ අහිමි වුණු 4.3%ක සම්පත් ප්‍රතිශතය 100%න් අඩු කරන්න වෙනවා.
මේ අනුව ශ්‍රී ලංකාවට හිම්වන සම්පත් ප්‍රතිශතය බවට පත්වෙන්නේ 95.7%ක්.
දැන් අපි ඒ අගයන් සියල්ලම මෙම සූත්‍රයට අන්තර්ගත කරමු.
281 * (95.7 / 100) + 1
මේ අනුව අපිට ලැබෙන පිළිතුර වන්නේ 269.91ක්.
මෙහි දී දශම ස්ථානයෙන් පසුව තිබෙන කිසිම අංකයක් ගණනය කිරීමකට ලක්වන්නේ නැහැ. ඒ අනුව තමයි එදා ශ්‍රී ලංකාවට ලැබුණු ජයග්‍රාහී ඉලක්කය ලකුණු 269ක් බවට පත්වුණේ. මෙම තරගය ඩක්වර්ත් ලුවිස් ස්ටර්න් ක්‍රමවේදය හඳුන්වා දීමට පෙර පැවති තරගයක් නිසා තමයි මෙම පිළිතුර හා ලැබුණ එදා ශ්‍රී ලංකාවට ලැබුණ ඉලක්කය සමාන අගයක් වුනේ.
6.3. Team B ඉනිම අතරතුර බාධා වී යළි තරගය ආරම්භ කිරීමට නොහැකි වීම.
අපි දැන් 2003 ලෝක කුසලානයට මතකය අවදි කරමු. එම ලෝක කුසලානයේ ශ්‍රී ලංකාව හා දකුණු අප්‍රිකාව අතර පැවති තරගය කාගේත් කතාබහට ලක්වුණු තරගයක්. දකුණු අප්‍රිකාවට 2003 ලෝක කුසලානයේ ඉදිරියටත් රැඳී සිටීමට නම් එම තරගයේ ජයග්‍රහණය ඔවුන්ට අනිවාර්යය කාරණයක් බවට පත්වෙලා තිබුණත් අවසානයේ තරගය ලකුණු සමවීමෙන් නිමාවට පත්වුනා.
මෙම තරගයේ මුලින්ම පන්දුවට පහර දුන් ශ්‍රී ලංකාව නියමිත පන්දුවාර 50 තුළ දී කඩුලු 9ක් දැවී ලකුණු 268ක් රැස්කරනු ලැබුවා. පසුව පිළිතුරු ඉනිම ක්‍රීඩා කළ දකුණු අප්‍රිකානු ඉනිමේ පන්දුවාර 45ක් අවසානයේ දී තරගයට වර්ෂාව පතිත වූ අතර තරගය නතර කරන විට ඔවුන් කඩුලු 5ක් දැවී ලකුණු 229ක් ලබා සිටියා.
ඩක්වර්ත් ලුවිස් ක්‍රමවේදයට අනුව පන්දුවාර 45ක් අවසානයේ දී ඔවුන් රැස්කර තිබිය යුතු ලකුණු සංඛ්‍යාව 230ක් වූවත්, ඒ පිළිබඳව තිබූ නොදැනුවත්භාවය නිසා මුත්තයියා මුරලිදරන් යැවූ අවසන් පන්දුවට මාක් බවුචර් ආරක්ෂාකාරී පහරක් එල්ල කළේ සත්කාරක දකුණු අප්‍රිකාවට තම ලෝක කුසලාන සිහිනයඳ බොඳ කරමින්.
අපි දැන් බලමු එලෙස පන්දුවාර 45ක දී දකුණු අප්‍රිකානුවන්ගේ ජයග්‍රාහී ඉලක්කය 230ක් බවට පත්වුණේ කොහොමද කියලා..
ඩක්වර්ත් ලුවිස් සූත්‍රයට අනුව එය ගණනය කරන්නේ මෙන්න මෙහෙමයි.
Target = S * (R2 / R1) + 1
මෙම තරගයේ මුලින් පන්දුවට පහර දුන් ශ්‍රී ලංකාව ලබා ගත්ත ලකුණු සංඛ්‍යාව 268ක් නිසා අපි S වශයෙන් 269 නමැති අගය සලකනු ලබනවා.
මෙහි දී ශ්‍රී ලංකා ඉනිම කිසිම බාධාවකින් තොරව නිමා ශ්‍රී ලංකාවට ලැබෙන සම්පත් ප්‍රමාණය වන්නේ 100%ක්. ඒ කියන්නෙ මෙතන R1 වෙන්නෙ 100%ක්.
දැන් අපි බලමු R2 හැදෙන්නේ කොහොමද කියලා,
පන්දුවාර 45ක දී වර්ෂාවෙන් බාධා ඇතිවෙලා තරගය නවත්වන මොහොතේ දකුණු අප්‍රිකානු කණ්ඩායමේ ලකුණු පුවරුව සටහන් වුනේ කඩුලු 6ක් දැවී ලකුණු 229ක් ලෙසයි. ඒ කියන්නෙ දකුණු අප්‍රිකාව සතුව එම මොහොතේ පන්දුවාර 5ක් සහ කඩුලු 4ක් අතැතිව තිබුණා.
ඊට අදාලව මෙම වගුවෙන් දකුණු අප්‍රිකානුවන්ට අහිමි වූ සම්පත් ප්‍රතිශතය වෙන්නේ 14.3%ක්. ඒ අනුව ඔවුන්ට හිමිවන සම්පත් ප්‍රමාණය 85.7%ක් බවට පත්වෙනවා. ඒ කියන්නේ 100%න් 14.3% අඩු කළාට පසුව ලැබෙන අගය තමයි 85.7%ක් වෙන්නේ.
දැන් අපි ඒ අගයන් සියල්ලම මෙම සූත්‍රයට අන්තර්ගත කරමු.
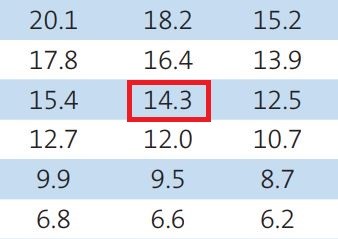
268 * (85.7 / 100) + 1
මේ අනුව අපිට ලැබෙන පිළිතුර වන්නේ 230.67ක්. කලින් කියපු විදිහට මෙතන දී දශම ස්ථානය ගණනය කිරීමට ලක් නොවන නිසා එදා දකුණු අප්‍රිකානුවන්ගේ ජයග්‍රාහී ඉලක්කය 230ක් බවට පත්වුණේ මෙන්න මෙහෙමයි.
6.4. Team B ඉනිම ප්‍රමාද වී ආරම්භ වීම.
අපි දැන් යන්නේ 2017 වසරේ ඉන්දීය කණ්ඩායමේ ශ්‍රී ලංකා සංචාරයේ පැවති දෙවැනි එක්දින තරගය දෙසට.
එම තරගයේ මුලින්ම පන්දුවට පහර දුන් ශ්‍රී ලංකාව නියමිත පන්දුවාර 50 තුළ දී කඩුලු 8ක් දැවී ලකුණු 236ක් රැස්කරනු ලැබුවා. පසුව තරගයට වර්ෂාව පතිත වී ඉන්දීය ඉනිම තරමක් ප්‍රමාද වී ආරම්භ වූයේ ඔවුන්ගේ ඉනිම පන්දු වාර 47කට සීමා කරමින්.
ඩක්ඩර්ත් ලුවිස් න්‍යායට අනුව ඔවුන්ට එම පන්දුවාර 47 තුළ ලකුණු 231ක ඉලක්කයක් හිමි වූ අතර ඉන්දියාව එම ජයග්‍රාහී ඉලක්කය පන්දුවාර 44.2ක දී සපුරා ගනු ලැබුවා. අපි දැන් බලමු මේ 231 හැදුණේ කොහොමද කියලා.
Target = S * (R2 / R1) + 1
මෙම තරගයේ මුලින් පන්දුවට පහර දුන් ශ්‍රී ලංකාව ලබා ගත්ත ලකුණු සංඛ්‍යාව 236ක් නිසා අපි S වශයෙන් 236 නැමැති අගය සලකනු ලබනවා.
මෙහි දී ශ්‍රී ලංකා ඉනිම කිසිම බාධාවකින් තොරව නිමා කළ නිසා අපි ඔවුන්ගේ සම්පත් ප්‍රමාණය 100%ක් වශයෙන් සලකනවා. ඒ කියන්නෙ මෙතන R1 වෙන්නෙ 100%ක්.
දැන් අපි බලමු R2 හැදෙන්නේ කොහොමද කියලා,
වර්ෂාවෙන් අනතුරුව තරගයේ පන්දුවාර 3ක් අඩු වුන නිසා මේ අනුව ඉන්දීය ඉනිම ආරම්භයට පෙර ඔවුන් අත ඉතිරිව තිබුණේ කඩුලු 10ක් සහ පන්දුවාර 47කුයි.
ඊට අදාලව මෙම වගුවෙන් ඉන්දියාවට හිමි වූ සම්පත් ප්‍රතිශතය වෙන්නේ 97.1%ක්.
දැන් අපි ඒ අගයන් සියල්ලම මෙම සූත්‍රයට අන්තර්ගත කරමු.
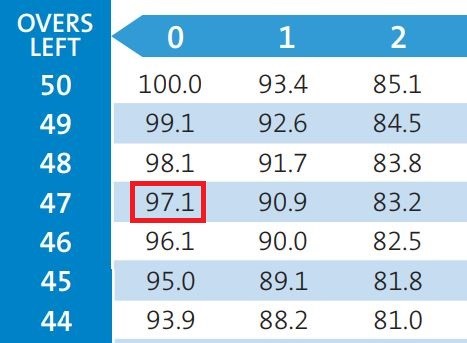
236 * (97.1% / 100%) + 1
මේ අනුව අපිට ලැබෙන පිළිතුර වන්නේ 230.15ක්.
මෙහි දී දශම ස්ථානයෙන් පසුව තිබෙන කිසිම අංකයක් ගණනය කිරීමකට ලක්වන්නේ නැති නිසා මෙහි අවසන් පිළිතුර වෙන්නේ 230ක්. නමුත් එදා ඔවුන්ට ලැබුණේ ලකුණු 231ක ඉලක්කයක්. ඒ තමයි මම කලින් සඳහන් කරපු පරිදී ඩක්වර්ත් ලුවීස් ස්ටර්න් සංශෝධනයට අනුව ලැබෙන පිළිතුර.
කලින් කියපු විදිහට එම පිළිතුරු අතර ඇත්තේ සුළු වෙනසක් නිසා මෙම තරගයේදි ස්ටර්න් සංශෝධනය මගින් යන්තම් එක ලකුණයි මෙතන දී වෙනස් වෙන්නේ.
අපි ඉතිරි උදාහරණ 2 සඳහා Team A Team B යනුවෙන් කණ්ඩායම් දෙකක් සම්බන්ධව උපකල්පනය කරමු.
6.5. තරගයේ බාධා වීම් කිහිපයක් සිදුවීම.
මෙහි දී මුලින්ම පන්දුවට පහර දුන් Team A නියමිත පන්දුවාර 50 තුළ දී ලකුණු 300ක් ලබා ගන්නවා. නමුත් Team B ඉනිම අතරතුර දෙවරක් බාධා වීම් සිදු වෙනවා.
මින් පළමු බාධා වීම සිදුවන්නේ Team B පන්දුවාර 15ක දී ලකුණු කඩුලු දෙකක් දැවී ලකුණු 80ක් ලබා සිටිය දීයි. ඉන්පසුව යළිත් තරගය ආරම්භ වන්නේ තවත් පන්දු වාර 5ක් අඩු කරමිනුයි.
ඒ අනුව අපි දැන් බලමු පන්දුවාර 45ක දී Team Bට ලැබුණු ඉලක්කය හැදෙන්නේ කොහොමද කියලා.
Target = S * (R2 / R1) + 1
මෙම තරගයේ මුලින් පන්දුවට පහර දුන් Team A ලබා ගත්ත ලකුණු සංඛ්‍යාව 300ක් නිසා අපි S වශයෙන් 300 නැමැති අගය සලකනු ලබනවා.
මෙහි දී Team A ඉනිම කිසිම බාධාවකින් තොරව නිමා කළ නිසා අපි ඔවුන්ගේ සම්පත් ප්‍රතිශතය 100%ක් වශයෙන් සලකනවා. ඒ කියන්නෙ මෙතන R1 වෙන්නෙ 100%ක්.
දැන් අපි බලමු R2 හැදෙන්නේ කොහොමද කියලා.
අපි කලින් කියපු විදිහට Team B ඉනිම ආරම්භයට පෙර ඔවුන්ගේ සම්පත් ප්‍රතිශතය වෙන්නෙත් 100%ක්.
නමුත් වර්ෂාව හේතුවෙන් තරගයට බාධා ඇති වන අවස්ථාවේ ඔවුන් අත ඉතිරිව පන්දුවාර 35ක් අතැතිව සහ කඩුලු 8ක් අතැතිව තිබූ නිසා තරගය නතර කරන අවස්ථාවේ ඔවුන් සතුව තිබූ සම්පත් ප්‍රතිශතය වෙන්නේ 73ක්.
නමුත් වර්ෂාවෙන් අනතුරුව තරගය පන්දුවාර 45කට සීමා වුණු නිසා Team B ක්‍රීඩා කිරීමට ඉතිරි වෙලා තිබෙන්නේ තවත් පන්දුවාර 30ක් සහ කඩුලු 8ක්. ඒ අනුව ඔවුන්ට නැවත තරගය ආරම්භ කරන අවස්ථාවේ ලැබෙන සම්පත් ප්‍රතිශතය වන්නේ 67.3ක්.
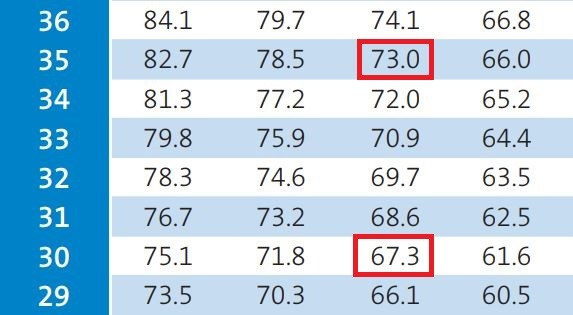
ඒ අනුව බාධා වීමෙන් අනතුරුව Team Bට අහිමි වන සම්පත් ප්‍රතිශතය වෙන්නේ 5.7ක්. (73-67.3) මේ නිසා දැන් Team Bට හිමි වන සම්පත් ප්‍රතිශතය වෙන්නේ 94.3ක්. (100-5.7)
දැන් අපි මේ අගයන් සියල්ලම මේ සූත්‍රයට දාමු.
300 * (94.3 / 100) + 1
මේ අනුව දැන් Team Bට පන්දු වාර 45කදී ලැබෙන ජයග්‍රාහී ඉලක්කය වෙන්නේ 283ක්
ඔන්න දැන් එකක් ඉවරයි. අපි යමු දැන් දෙවැනි අවස්ථාවට.
නමුත් තරගය ආරම්භ වෙලා Team B තවත් පන්දුවාර 10ක් ක්‍රීඩා කළාට පස්සේ ආයෙත් වර්ෂාව හරස්වෙනවා. ඒ අනුව දෙවන වර තරගය නතර කරන විට පන්දුවාර 25ක දී ඔවුන්ගේ ලකුණු පුවරුව දැක්වුණේ 140/3ක් ලෙසින්. ඉන්පසු යළිත් තරගය ආරම්භ වෙන්නේ තවත් පන්දුවාර 5ක් අඩු කරමින්.
ඒ කියන්නේ Team Bට පන්දුවාර 40ක් තුළ ලබා ගත යුතු නව ඉලක්කය තමා අපි දැන් ගණනය කරන්නේ.
දෙවන වර වර්ෂාව හේතුවෙන් තරගයට බාධා ඇති වන අවස්ථාවේ ඔවුන් අත ඉතිරිව පන්දුවාර 20ක් සහ කඩුලු 7ක් අතැතිව තිබූ නිසා තරගය නතර කරන අවස්ථාවේ ඔවුන් සතුව තිබූ සම්පත් ප්‍රතිශතය වෙන්නේ 49.1ක්.
නමුත් වර්ෂාවෙන් අනතුරුව තරගය යළිත් පන්දුවාර 40කට සීමා වුණු නිසා Team B ක්‍රීඩා කිරීමට ඉතිරි වෙලා තිබෙන්නේ තවත් පන්දු වාර 15ක් සහ කඩුලු 7ක්. ඒ අනුව ඔවුන්ට නැවත තරගය ආරම්භ කරන අවස්ථාවේ ලැබෙන සම්පත් ප්‍රතිශතය වන්නේ 40.5ක්.
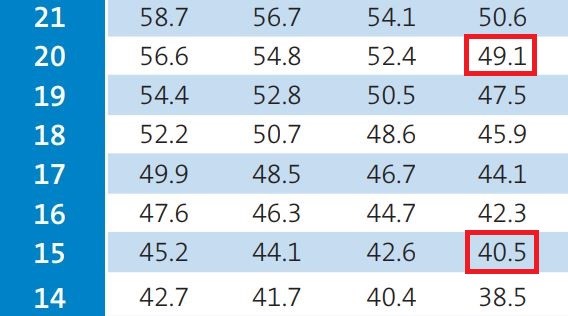
ඒ අනුව දෙවැනි බාධා වීමෙන් අනතුරුව Team Bට අහිමි වන සම්පත් ප්‍රතිශතය වෙන්නේ 8.6ක්. (49.1-40.5)
ඔබට මතක ඇති අපි පළමු වර බාධා වීමේ දී අහිමි වූ සම්පත් ප්‍රතිශතය අපි 100%න් අඩු කළා කියලා. අපි පෙර වතාවල් වලදි අම අගය ඒ 100%න් අඩු කළේ ඊට පෙරාතුව ඉනිමට කිසිදු බාධාවක් සිදු වෙලා නැති නිසා. නමුත් මේ ලෙසින් දෙවන වර බාධා වුවහොත් අපි එම අහිමි වූ ප්‍රතිශතය අඩු කරනු ලබන්නේ පළමු බාධා වීමෙන් පසුව Team Bට හිමි වූ සම්පත් ප්‍රතිශතයෙන්. ඒ කියන්නේ 94.3න්.
මේ අනුව දැන් Team Bට හිමි වන සම්පත් ප්‍රතිශතය ගණනය කිරීමට නම් ඔවුන්ට දෙවන වර අහිමි වූ 8.6ක සම්පත් ප්‍රතිශතය 94.3න් අඩු කරන්න සිදු වෙනවා. ඒ අනුව ලැබෙන පිළිතුර වෙන්නේ 85.7ක්. (94.3-8.6)
දැන් අපි මේ අගයන් සියල්ලම මේ සූත්‍රයට දාමු.
300 * (85.7 / 100) + 1
මේ අනුව දැන් Team Bට පන්දුවාර 40ක දී ලැබෙන නව ජයග්‍රාහී ඉලක්කය වෙන්නේ 258ක්. මෙන්න මෙහෙම තමයි ඩක්වර්ත් ලුවිස් මගින් එකම ඉනිමේ බාධා වීම් සිදු වූ අවස්ථා දෙකක දී ජයග්‍රාහී ඉලක්කයන් හැදෙන්නේ.
6.6. Team A ඉනිම අතරතුර දී බාධා ඇතිවී ඉනිම අවසන් කිරීමට සිදු වීම සහ Team B ඉනිම ආරම්භ වීමට ප්‍රමාද වීම.
මෙහි දී මුලින්ම පන්දුවට පහර දුන් Team A පන්දුවාර 47ක දී කඩුලු 6ක් දැවී ලකුණු 280ක් ලබා සිටිය දී වර්ෂාව හරස් වීමෙන් පසුව එම ඉනිම යළිත් ක්‍රියාත්මක කිරීමට නොහැකි වූ අතර Team B ඉනිමත් පන්දුවාර 30කට සීමා වුනා. ඒ අනුව Team Bට ලැබෙන ජයග්‍රාහී ඉලක්කය තමයි අපි දැන් ගණනය කරන්නේ.
මෙහි දී Team A ඉනිම ආරම්භයට පෙර ඔවුන්ට හිමිව තිබූ සම්පත් ප්‍රතිශතය වන්නේ 100%ක්. නමුත් Team A ඉනිම පන්දුවාර 47ක දී අවසන් කිරීමට සිදු වන විට ඔවුන් සතුව පන්දුවාර 3ක් සහ කඩුලු 4ක් අතැතිව තිබූ නිසා ඔවුන්ට ඒ අනුව අහිමි වන සම්පත් ප්‍රතිශතය වන්නේ 9.5%ක්.
ඒ අනුව අපි දැන් ආරම්භයේ තිබූ සම්පත් ප්‍රතිශතය වුන 100%න් එම 9.5% අඩු කරනවා. ඒ කියන්නෙ මෙතන R1 වෙන්නෙ 90.5%ක් (100%-9.5%).
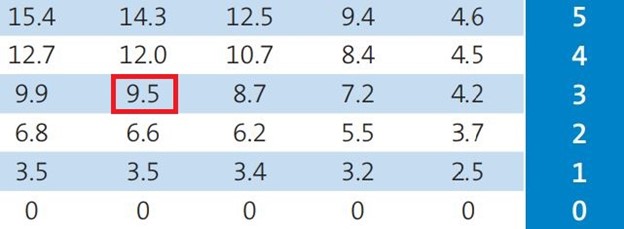
දැන් අපි බලමු R2 හැදෙන්නෙ කොහොමද කියලා.
වර්ෂාවෙන් අනතුරුව Team B ඉනිමත් පන්දුවාර 30කට සීමා වුන නිසා ඔවුන්ට ලැබෙන සම්පත් ප්‍රතිශතය වන්නේ 75.1%ක්. මෙහි දී ඔවුන් අතැති පන්දුවාර සංඛ්‍යාව 30ක් සහ අතැති කඩුලු සංඛ්‍යාව 10ක් නිසා ඒ අනුව තමයි අපි මෙම වගුවෙන් 75.1%ක ප්‍රතිශත අගය R2 සඳහා ලබා ගන්නේ.
දැන් අපි ඉහත අගයන් මෙම සූත්‍රයට ආදේශ කරමු.
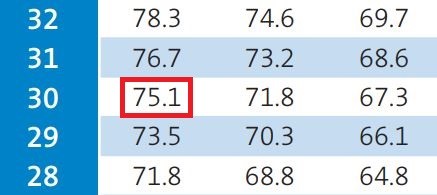
280 * (75.1 / 90.5) + 1
මේ අනුව මෙම තරගයේ Team Bට පන්දු වාර 30ක දී ලැබෙන ජයග්‍රාහී ඉලක්කය වෙන්නේ 233ක්.
—
මෙන්න මේ ආකාර 6ට අනුව තමයි පුරා දශක දෙකකටත් වැඩි කාලයක් පුරාවටම එක්දින ජාත්‍යන්තර තරග රටාවේ භාවිතා කළ ඩක්ඩර්ත් ලුවිස් න්‍යායේ ගණනය කිරීම් සිදු වුනේ.
එම කාලපරිච්ඡේදය තුළ පැවති බාධා ඇති වූ බොහෝ තරගවලට නිශ්චිත ප්‍රතිඵලයක් ලබා දීමට ඒ මගින් හැකි වීම සමස්ත ක්‍රිකට් ක්‍රීඩාවේම විශාල ජයග්‍රහණයක් වශයෙන් අපට හඳුන්වන්න පුළුවන්.
>> තවත් විශේෂාංග ලිපි සඳහා පිවිසෙන්න <<
